Large-Scale Bounded Distortion Mappings
Shahar Kovalsky, Noam Aigerman, Ronen Basri and Yaron Lipman
Siggraph Asia 2015
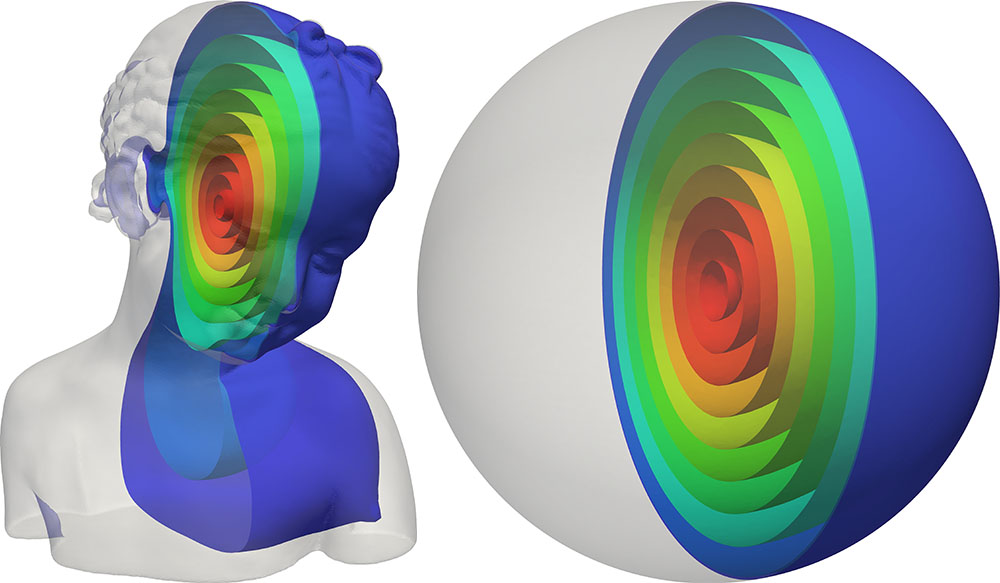

We propose an efficient algorithm for computing large-scale bounded distortion maps of triangular and tetrahedral meshes. Specifically, given an initial map, we compute a similar map whose differentials are orientation preserving and have bounded condition number.
Inspired by alternating optimization and Gauss-Newton approaches, we devise a first order method which combines the advantages of both. On the one hand, its iterations are as computationally efficient as those of alternating optimization. On the other hand, it enjoys preferable convergence properties, associated with Gauss-Newton like approaches.
We demonstrate the utility of the proposed approach in efficiently solving geometry processing problems, focusing on challenging large-scale problems.
Just a teaser... download the paper if you want all the details.
Given a mapping \(\Phi_0\) of a triangular or tetrahedral mesh:
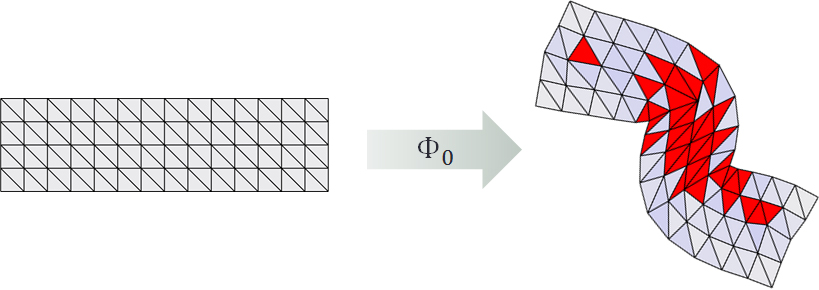
Efficiently compute a similar bounded-distortion mapping \(\Phi_0\):
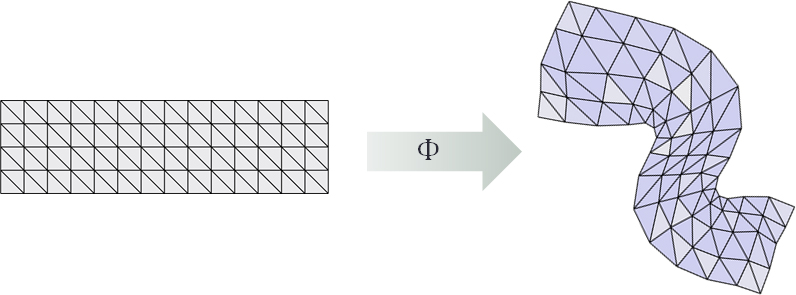
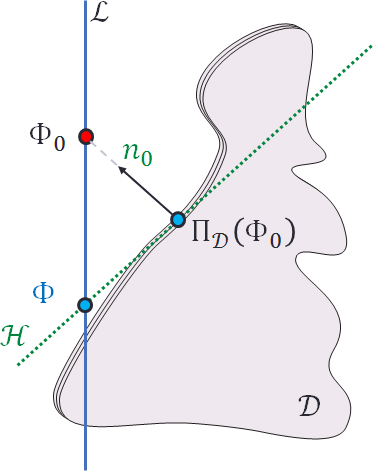
Use a single hyperplane \(\mathcal{H}\) as a first order proxy for the set of bounded distortion mappings \(\mathcal{D}\).
And repeat the following steps:
1. Compute the projection onto bounded distortion \(\Pi_\mathcal{D}(\Phi_0)\).
2. Form the hyperplane
\[
\mathcal{H} = \left\{ x : n_0^Tx = n_0^T (\Pi_\mathcal{D}(\Phi_0) \right\}
\]
3. Solve
\[
\begin{align}
\min_{\Phi} & \left\| \Phi-\Pi_\mathcal{D}(\Phi_0) \right\| \\
\mathrm{s.t.} & \Phi \in \mathcal{H}\cap\mathcal{L}\\
\end{align}
\]
This last step boils down to the solution of a simple KKT linear system, which can be efficiently solved using prefactorization. The resulting algorithm is very efficient and highly competitive with related approaches:
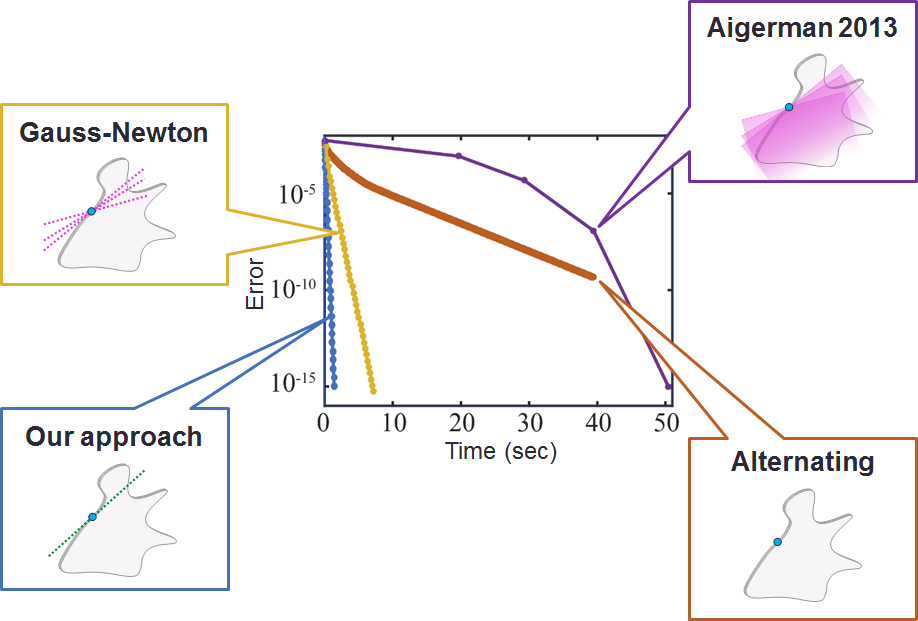
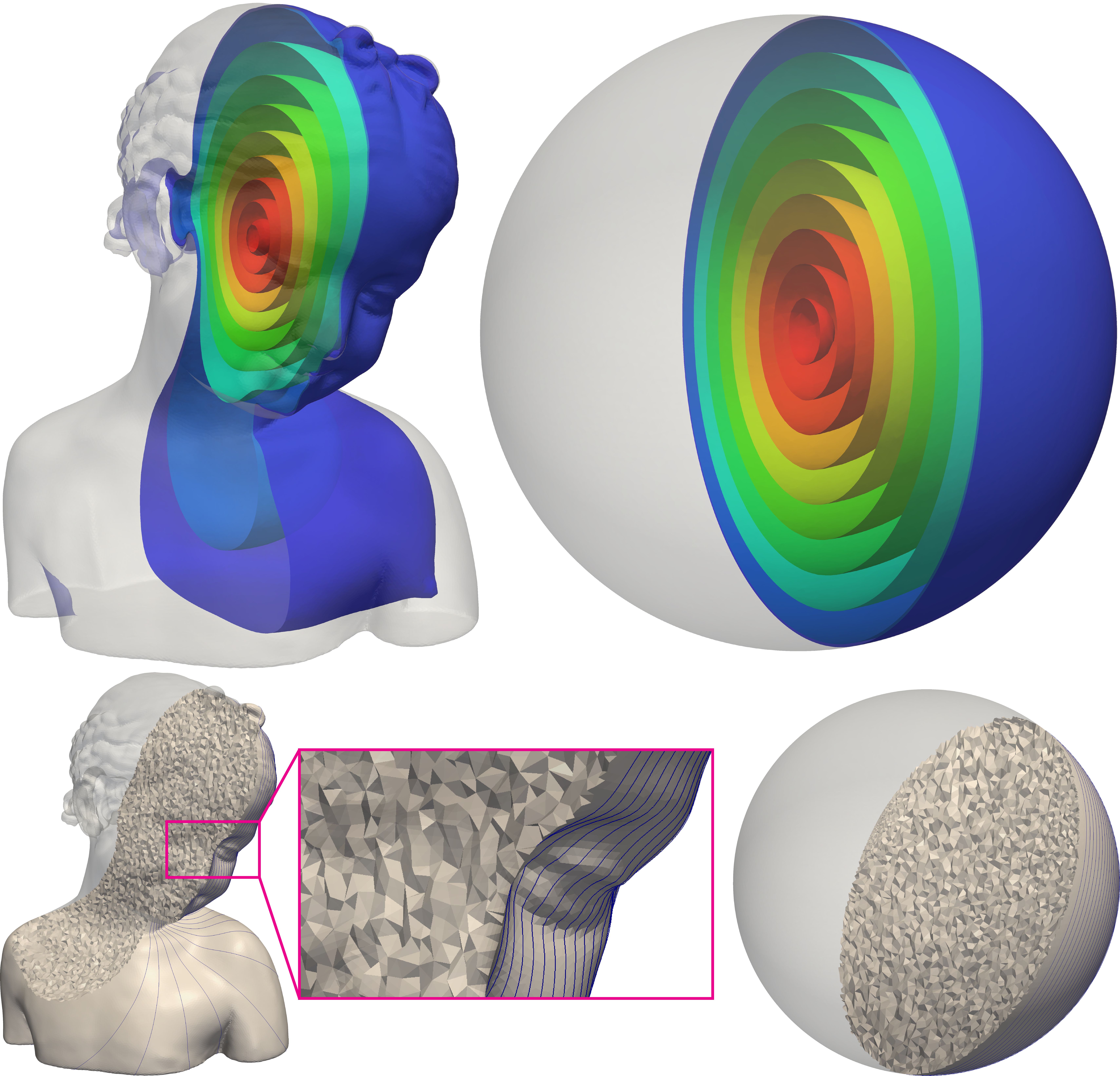
Compute bijective and bounded-distortion mappings between 3D meshes comprising over 1 million tetrahedra:
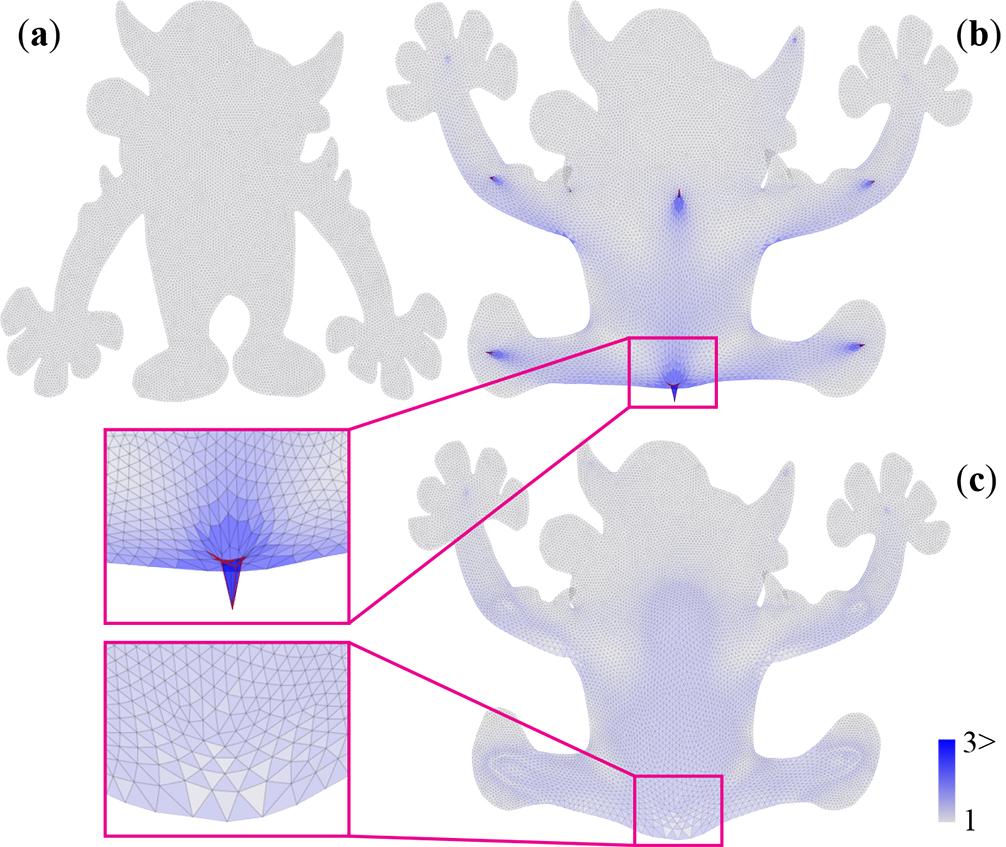
Efficiently compute bounded distortion deformations:
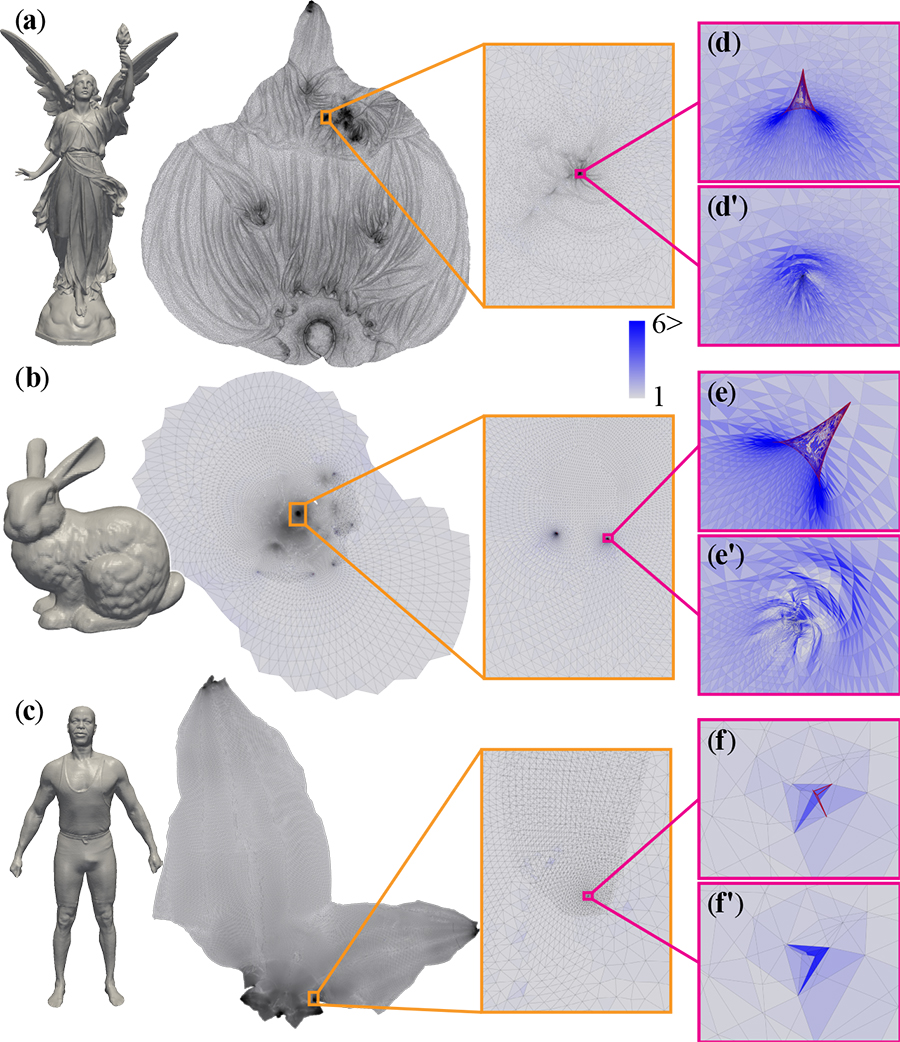
Compute bounded-distortion parameterizations of high-resolution surfaces:
A Matlab implementation of the paper can found on GitHub. A zip file of the latest version can be directly downloaded here.
This package includes three examples:
The input to all examples are randomly generated mappings that have high distortions and flipped elements.
Compatibility: The code was tested with Matlab (2014b). The code depends on two mex files, currently only Windows (x64) is supported. Please contact me regarding running the code on other platforms.
Disclaimer: The code is provided as-is for academic use only and without any guarantees. Please contact the author to report any bugs.
@article{LargeScaleBD:2015,
author = {Kovalsky, Shahar Z. and Aigerman, Noam and Basri, Ronen and Lipman, Yaron},
title = {Large-scale bounded distortion mappings},
journal = {ACM Transactions on Graphics (proceedings of ACM SIGGRAPH Asia)},
volume = {34},
number = {6},
year = {2015},
}