Controlling the singular values of n-dimensional matrices is often required in geometric algorithms in graphics and engineering. This paper introduces a convex framework for problems that involve singular values. Specifically, it enables the optimization of functionals and constraints expressed in terms of the extremal singular values of matrices.

Towards this end, we introduce a family of convex sets of matrices whose singular values are bounded. These sets are formulated using Linear Matrix Inequalities (LMI), allowing optimization with standard convex Semidefinite Programming (SDP) solvers. We further show that these sets are optimal, in the sense that there exist no larger convex sets that bound singular values.

A number of geometry processing problems are naturally described in terms of singular values. We employ the proposed framework to optimize and improve upon standard approaches. We experiment with this new framework in several applications: volumetric mesh deformations, extremal quasi-conformal mappings in three dimensions, non-rigid shape registration and averaging of rotations. We show that in all applications the proposed approach leads to algorithms that compare favorably to state-of-art algorithms.

Just a teaser... download the paper if you want all the details.

Our goal

Solve optimization problem explicitly expressed in terms of matrices and their extermal singular values: \[ \begin{align} \min_{A\in\mathbb{R}^{n\times n}} & \quad f(A,\sigma_\mathrm{min}(A),\sigma_\mathrm{max}(A)) \\ \mathrm{s.t.} & \quad g_i(A,\sigma_\mathrm{min}(A),\sigma_\mathrm{max}(A))\leq 0\, , \quad i=1,..,r \\ \end{align} \] where \(f\) and \(g_i\) are convex and satisfy simple monotonicity conditions.

For example, find a matrix \(A\) which is the closest to a given matrix \(B\) and deviates by at most \(\Gamma\) from an isometry: \[ \begin{align} \min_{A\in\mathbb{R}^{n\times n}} & \quad \left\|A-B\right\|_F\\ \mathrm{s.t.} & \quad \Gamma^{-1} \leq \sigma_\mathrm{min}(A) \leq \sigma_\mathrm{max}(A) \leq \Gamma\\ \end{align} \]

The idea

Formulate convex bounds on the extremal singular values \(\sigma_\mathrm{min}(A)\) and \(\sigma_\mathrm{max}(A)\).

Bounding \(\sigma_\mathrm{max}(A)\) is readily convex and can be written as an LMI (positive semidefinite constraint): \[ \sigma_\mathrm{max}(A)\leq\Gamma \quad \Leftrightarrow \begin{pmatrix} \Gamma I & A \\ A^T & \Gamma I \\ \end{pmatrix}\succeq 0 \]

Bounding \(\sigma_\mathrm{min}(A)\) is non-convex, but can be also imposed by an LMI: \[ \sigma_\mathrm{min}(A)\geq\gamma \quad \Leftarrow \quad \frac{A+A^T}{2} \succeq \gamma I \] This characterizes a maximal convex subset of the bound.

Moreover, by simply rotating \(A\) it spans a maximal convex cover of the bound.

Semidefinite programming (SDP) can be used to enforce both constraints.

Applications

Volumetric meshes

Optimize problems with energies and constraints expressed in terms of singular values:

Extremal quasiconformal mappings

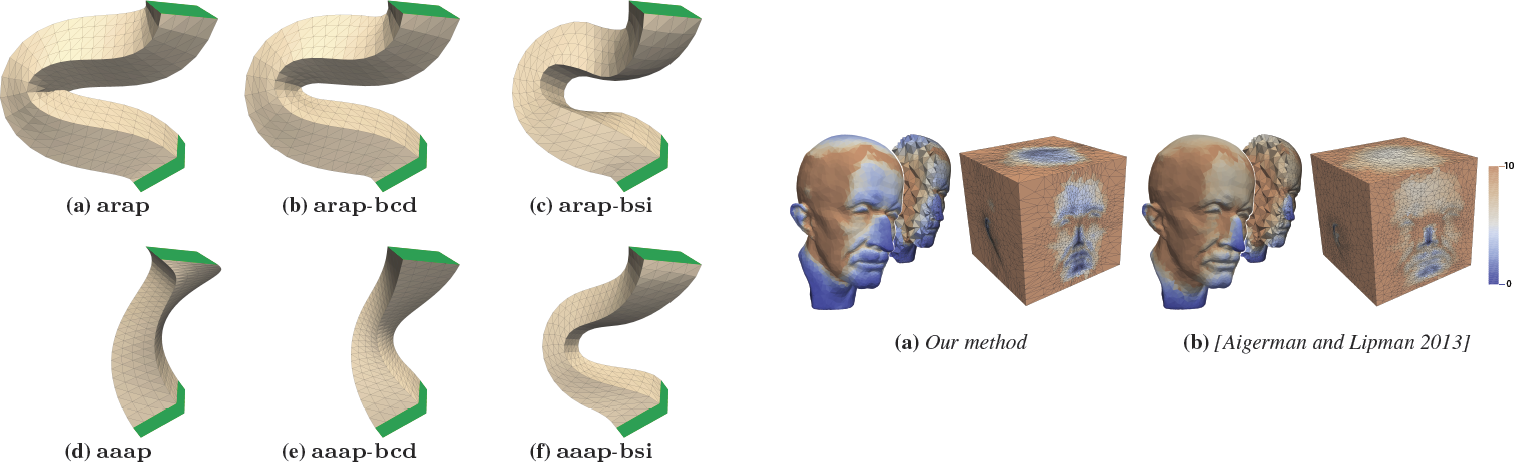
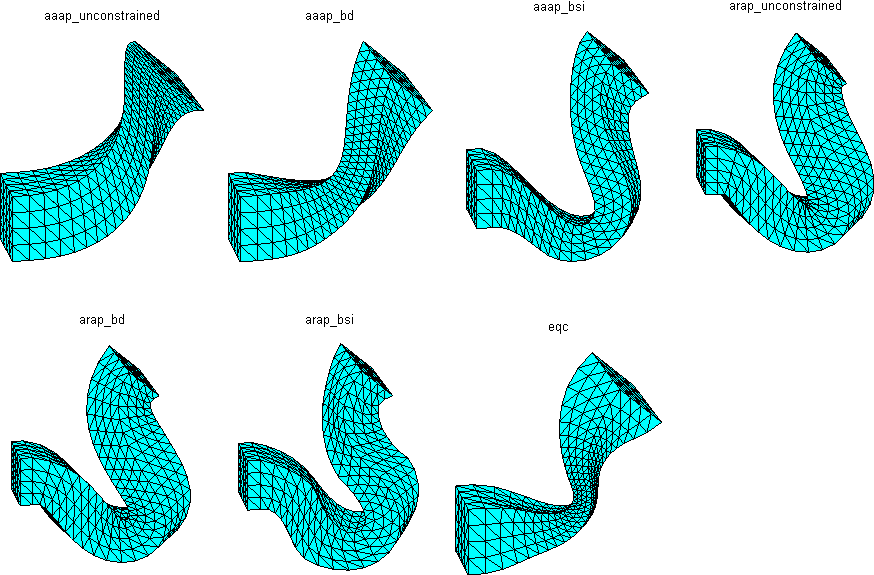
Compute mapping that minimize the maximal conformal distortion:

Non-Rigid 3D Registration

Improve a basic ICP algorithm for surface matching -- restrict deviations from isometry to directly control distortion:

Averaging of rotations

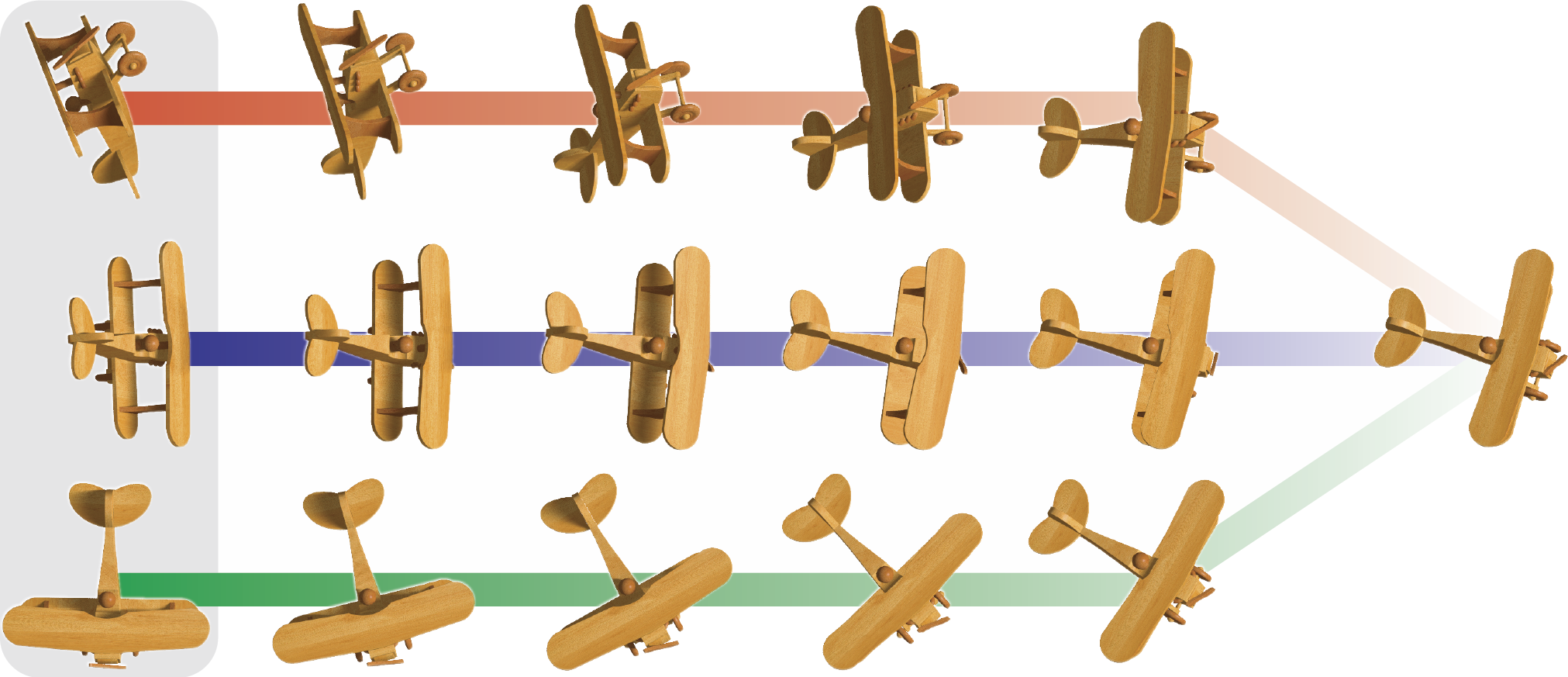
Average (and interpolate) multiple rotations:

A Matlab implementation of the paper can found on GitHub. A zip file of the latest version can be directly downloaded here.

This package includes three examples:

• example_optimizeSingleMatrix.m demonstrates simple single matrix optimization problems with constraints on singular values. Algorithm 1 of the paper is applied to a few example optimization problems, aiming to illustrate the implementation and usage of the theory presented in the paper (section 4 and 5).
• example_BarDeformation.m demonstrates volumetric mesh optimization problems with constraints on singular values. Algorithm 2 of the paper is applied to some example optimization problems, generating some of the example deformations of Figure 2 in the paper. See section 6.1 in the paper for additional details. Either run the entire code for generating all examples (might take a while), or the relevant code block for your desired example.

• example_ExtremalQuasiConformal.m implements an algorithm for computing extremal quasiconformal mappings of volumetric meshes (i.e., minimizing maximal conformal distortion). The code reproduces the example presented in Figure 1. See section 6.1 for additional details.

Getting started: Before running the code, make sure you have YALMIP and MOSEK installed. Update the paths in initialize.m accordingly. The code was tested with Matlab (2013a), YALMIP (20140915) and MOSEK (7.0.0.92).

Disclaimer: The code is provided as-is for academic use only and without any guarantees. Please contact the authors to report any bugs.

@article{ContSingVal:2014,
author = {Kovalsky, Shahar Z. and Aigerman, Noam and Basri, Ronen and Lipman, Yaron},
title = {Controlling Singular Values with Semidefinite Programming},
journal = {ACM Transactions on Graphics (proceedings of ACM SIGGRAPH)},
volume = {33},
number = {4},
year = {2014},
}